Linear Mixed Effects Models in R

An introduction for linguistic students

Chenzi Xu

University of Oxford

2021/12/12 (updated: 2022-02-18)

chenzi.xu@rbind.io

1 / 47

Find me at...

@ChenziAmy
@chenchenzi
chenzixu.rbind.io

2 / 47

Did you do the pre-workshop setup?

https://chenzixu.rbind.io/talk/lme/

We assume:

You have basic knowledge about R and R studio.

You have basic inferential statistical knowledge.

You want to know more about linear mixed models

3 / 47

high school arithmetic and algebra. Elementary concepts of probability theory are assumed; the sum and the product rules, and the fact that the probabilities of all possible events must sum to 1, are the extent of the knowledge assumed.

Outline

Inferential Stats Recap
Linear Regression
Linear Mixed Effects Models
Shrinkage in linear mixed models
Report Writing
Why LME model?

4 / 47

Inferential Stats Recap5 / 47

Inferential Stats Recap

Central limit theorem (~~magic~~)

Hypothesis testing: the (humble) t-test

5 / 47

Central limit theorem (magic)

Definition and Significance

The picture is from Wikipedia.

The sampling distribution of means is normal, provided two conditions are met: (a) the sample size should be large enough (b) $μ$ and $σ$ are defined for the probability density or mass function that generated the data.

We can derive an estimate of the distribution of (hypothetical) sample means from a single sample of n independent data points

CLT is NOT the distribution that generated the data, but the sampling distribution of the sample means under repeated sampling.

6 / 47

SE estimates how much error there is, across repeated sampling, in our estimate of the population mean using sample mean. Our estimation will be more precise for larger sample size or lower variability.

Hypothesis testing: the (humble) t-testNHST procedure
Define the null hypothesis μ0μ0
Given data of size nn, estimate ¯yy¯, standard deviation ss, estimate the standard error SE=s/√nSE=s/n.
The distance between the sample mean and the hypothesized mean can be written in SE units as follows.t×SE=¯y−μt×SE=y¯−μ
Thus the sample mean is t standard errors away from the hypothesized mean: t=¯y−μ0s/√nt=y¯−μ0s/n
Reject null hypothesis if the observed t-value is “large”.
Fail to reject the null hypothesis, if the observed t-value is “small”.

7 / 47

One of the simplest statistical tests that one can do with continuous data: the t-test. the logic of these more complex tests will essentially be more of the same

uncertainty in the estimates of the values as the scale on which distances are measured.

Hypothesis testing: the (humble) t-test

Under repeated sampling, the observed t-value is seen as an instance from a random variable T. $T \sim t (n - 1)$ The PDF of T, the t-distribution, is defined in terms of of n with n-1 degrees of freedom.

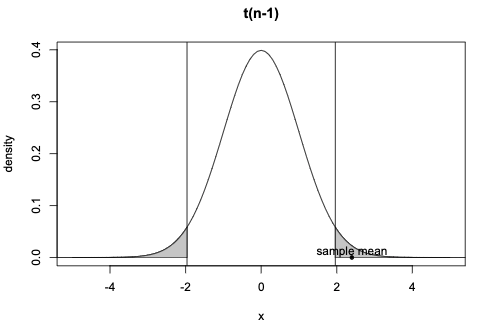
Critical t-value: the t-value such that $P (T > | t |) = 0.05$

Type I error: Reject the null when it’s true Type II error: Fail to reject the null when it’s false

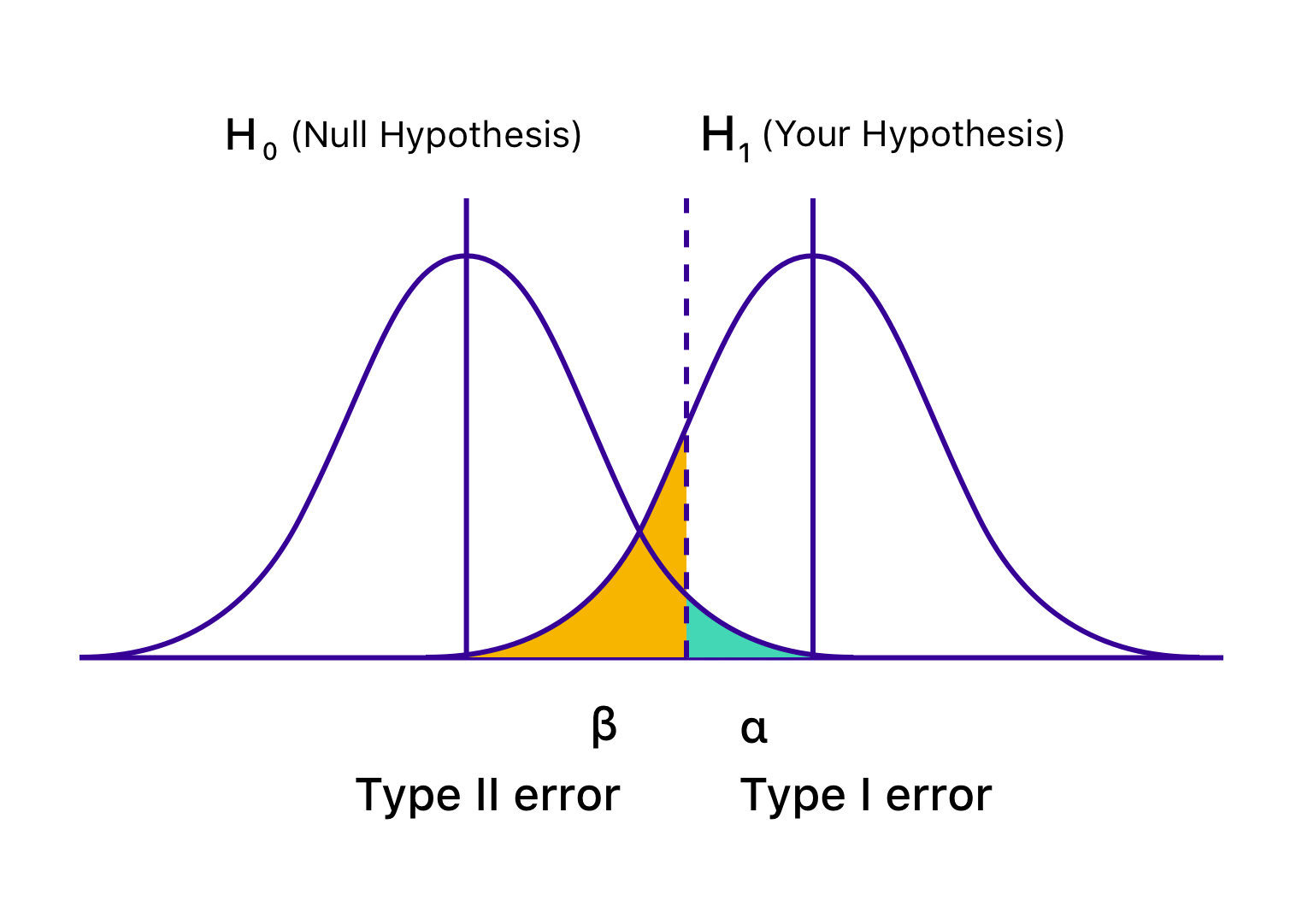
p-value: the probability of obtaining the observed t-value, or some value more extreme than that, under the assumption that the null is true.

The p-value is always interpreted with reference to the pre-defined Type I error. Conventionally, we reject the null if $p < 0.05$

8 / 47

Two possible decisions: reject the null or fail to reject the null. Two possible worlds: the null is true or false. The first picture is from Vasishth's book; The second picture is from https://vwo.com/blog/errors-in-ab-testing/

The t-test is just a special, limited example of a general linear model. ANOVA is also a special, limited version of the linear model.(categorical predictors. more than two levels.) general linear model: A mathematical model comparing how one or more independent variables affect a continuous dependent variable.

df measures number of pieces of independent information that go into estimateing some parameters.

p-values are NOT the probability the null hypothesis is true, and does not measure strength of an effect.

Linear Regression9 / 47

Linear Regression

Formal forms

A (too) simple case study

Understanding output

Assumptions check

9 / 47

Formal forms

A simple example of linear model is $Y_{i} = β_{0} + β_{1} X_{i} + e_{i}$ Where $Y_{i}$ is the measured value of the dependent variable for observation i; $X_{i}$ is the explanatory variable or predictor; $Y_{i}$ is modelled in terms of an intercept $β_{0}$ plus the effect of predictor $X_{i}$ weighted by coefficient $β_{1}$ and error term $e_{i}$ .

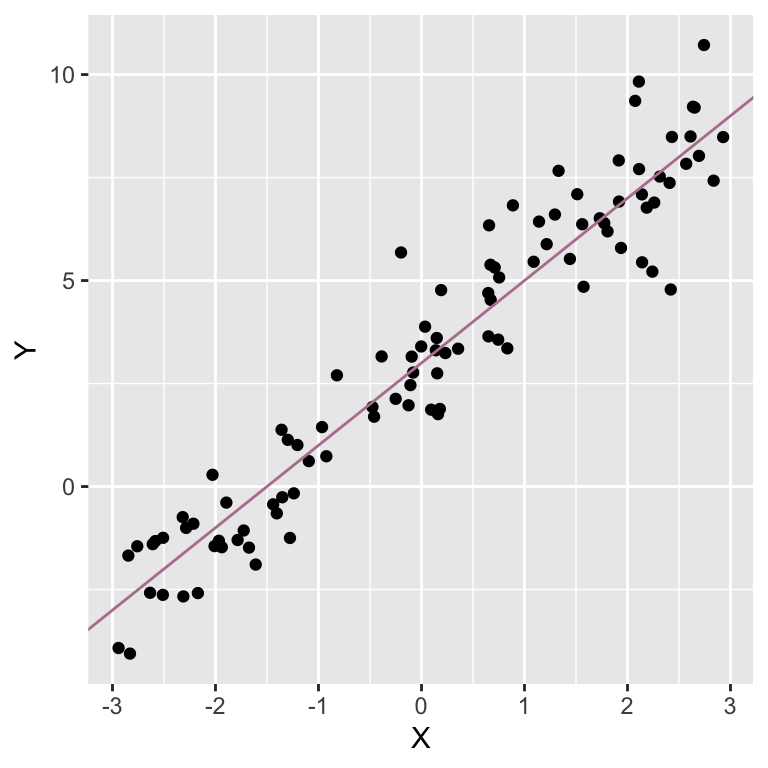
Simulated data illustrating linear model $Y_{i} = 3 + 2 X_{i} + e_{i}$ . The most common method for fitting a regression line is least-squares.

A linear model is a model that is linear in the coefficients; each coefficient is only allowed to be set to the power of one.

Non-linear relationships can be analysed using a linear model.

10 / 47

LME an extension of the General Linear Model that underlies simpler approaches such as ANOVA, t-test, and classical regression. Many people assume that 'linear models' can only capture linear relationships, i.e., relationships that can be described by a straight line (or a plane). This is false. A linear model is a weighted sum of various terms, and each term has a single predictor (or a constant) that is multiplied by a coefficient.

A simple case study

Research question

Assume you were interested in whether the voice pitch of males and females differs, and if so, by how much.

Data

pitch = c(233,204,242,130,112,142)
sex = c(rep("female",3), rep("male",3))
my.df = data.frame(sex,pitch)
my.df

#      sex pitch
# 1 female   233
# 2 female   204
# 3 female   242
# 4   male   130
# 5   male   112
# 6   male   142

Formula

Relationship of interest $p i t c h \sim s e x$

"Pitch predicted by / as a function of sex" $p i t c h \sim s e x + ϵ$ $ϵ$ stands for all other things that affect pitch, random or controllable in our experiment. Structural or systematic + random or probabilistic

model = lm(pitch ~ sex, my.df)
contrasts(as.factor(my.df$sex))

##        male
## female    0
## male      1

Dummy coding for categorical factors

This example is taken from Bodo Winter's tutorial.

11 / 47

Dummy coding for categorical factors contrasts(as.factor(my.df$sex))

Understanding output

summary(model)

# 
# Call:
# lm(formula = pitch ~ sex, data = my.df)
# 
# Residuals:
#       1       2       3       4       5       6 
#   6.667 -22.333  15.667   2.000 -16.000  14.000 
# 
# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)   226.33      10.18  22.224 2.43e-05 ***
# sexmale       -98.33      14.40  -6.827  0.00241 ** 
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Residual standard error: 17.64 on 4 degrees of freedom
# Multiple R-squared:  0.921,    Adjusted R-squared:  0.9012 
# F-statistic: 46.61 on 1 and 4 DF,  p-value: 0.002407

$R^{2}$ : "variance accounted for or explained by"

Multiple R-Squared: how much variance in our data is accounted for by our model

Adjusted R-Squared: how much variance is “explained” and how many fixed effects are used

p-value: The probability of our data, given that our null hypothesis "sex has no effect on pitch" is true.

Reporting:

We constructed a linear model of pitch as a function of sex. This model was significant $(F (1, 4) = 46.61, p < 0.01)$ .

12 / 47

Understanding output

summary(model)

# 
# Call:
# lm(formula = pitch ~ sex, data = my.df)
# 
# Residuals:
#       1       2       3       4       5       6 
#   6.667 -22.333  15.667   2.000 -16.000  14.000 
# 
# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)   226.33      10.18  22.224 2.43e-05 ***
# sexmale       -98.33      14.40  -6.827  0.00241 ** 
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Residual standard error: 17.64 on 4 degrees of freedom
# Multiple R-squared:  0.921,    Adjusted R-squared:  0.9012 
# F-statistic: 46.61 on 1 and 4 DF,  p-value: 0.002407

mean(my.df[my.df$sex=="female",]$pitch)

# [1] 226.3333

mean(my.df[my.df$sex=="male",]$pitch)

# [1] 128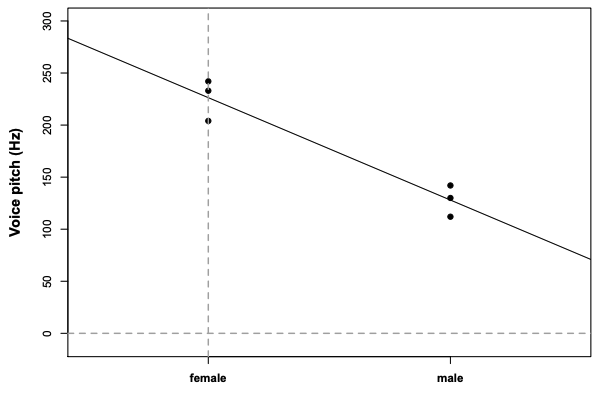

13 / 47

Assumptions check

(1) Linearity

The fitted values (line) are the predicted means, and residuals are the vertical deviations from this line.

When the residual plot shows a curvy or non-linear patterns, it indicates a violation of the linearity assumption.

plot(fitted(model),residuals(model))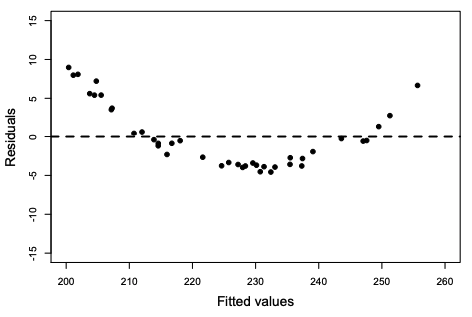

What to do if your residual plot indicates nonlinearity?

Reconsider the fixed effects
Perform non-linear transformation of your variables
Turn to different class of models such as logistic models

14 / 47

conditions that have to be satisfied in order for the linear model to be meaningful.

Assumptions check

(2) Absence of collinearity

When two predictors are correlated with each other, they are collinear.

Preempt the problem in the design stage
Use dimension reduction techniques such as Principal Component Analysis that transform correlated variables into a smaller set of variables

(3) Homoskedasticity

The variance of your data should be approximately equal across the range of the predicted values.

Transform your data

15 / 47

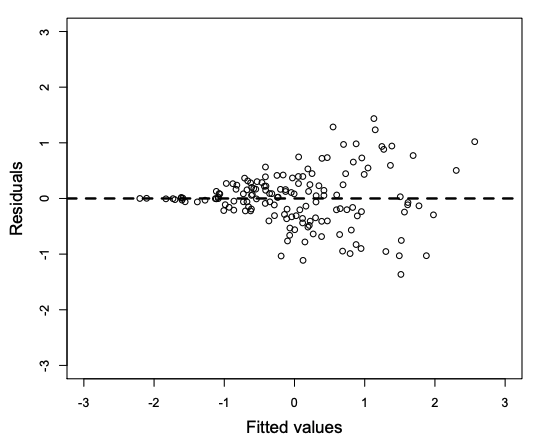
Assumptions check

(4) Absence of influential data points

dfbeta(model)

#     (Intercept)   sexmale
# 1  3.333333e+00 -3.333333
# 2 -1.116667e+01 11.166667
# 3  7.833333e+00 -7.833333
# 4 -1.359740e-16  1.000000
# 5  1.087792e-15 -8.000000
# 6 -9.518180e-16  7.000000

DFbeta values: the coefficients to be adjusted if a particular data point is excluded (“leave-one-out diagnostics”).

Eyeball the DFbeta values: any sign changed? different by half of the absolute value?
Run the analysis with influential data and then again without them. Compare and discuss the results.

dfbeta() for linear models doesn’t work for mixed models. You can check out the package influence.ME (Nieuwenhuis, te Grotenhuis, & Pelzer, 2012), or program a for loop that does the leave-one-out diagnostics by hand.

16 / 47

Assumptions check

(5) Normality of residuals

a histogram or a Q-Q plot of the residuals

hist(residuals(model))
qqnorm(residuals(model))

(6) Independence

Preempt the problem in the design stage
Resolve non-independencies at the analysis stage. $\to$ Mixed models

17 / 47

Linear Mixed Effects Model18 / 47

Linear Mixed Effects Model

Data

Model

Assumption

Understanding the output

Model selection

18 / 47

Data

Research Question

We're interested in the relationship between pitch and politeness (Winter & Grawunder, 2012).

Politeness: formal/polite and informal register (categorical factor)
multiple measures per subject (inter-dependent!)

data = read.csv("http://www.bodowinter.com/tutorial/politeness_data.csv")
head(data)

#   subject gender scenario attitude frequency
# 1      F1      F        1      pol     213.3
# 2      F1      F        1      inf     204.5
# 3      F1      F        2      pol     285.1
# 4      F1      F        2      inf     259.7
# 5      F1      F        3      pol     203.9
# 6      F1      F        3      inf     286.9

which(!complete.cases(data))

# [1] 39

19 / 47

a few missing values provide no problems for our mixed model analyses

Model

Linear regression $p i t c h \sim p o l i t e n e s s + ϵ$ Multiple regression (fixed effects only) $p i t c h \sim p o l i t e n e s s + s e x + ϵ$ Add a random effect for subject: assume a different "baseline" pitch value for each subject. We can assume different random intercepts for each subject. $p i t c h \sim p o l i t e n e s s + s e x + (1 | s u b j e c t) + ϵ$

boxplot(frequency~subject, data)

Crossed random effects for subjects and for items. Different scenarios for formal and informal speech (by-item variation) $p i t c h \sim p o l i t e n e s s + s e x + (1 | s u b j e c t) + (1 | i t e m) + ϵ$

20 / 47

Model in R

library(lme4)
data = data %>% mutate(attitude=as.factor(attitude), gender=as.factor(gender), subject=as.factor(subject))
politeness.model0 = lmer(frequency ~ attitude + (1|subject) + (1|scenario), data=data)
politeness.model = lmer(frequency ~ attitude + gender + (1|subject) + (1|scenario), data=data)
summary(politeness.model)

# Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
# Formula: frequency ~ attitude + gender + (1 | subject) + (1 | scenario)
#    Data: data
# 
# REML criterion at convergence: 775.5
# 
# Scaled residuals: 
#     Min      1Q  Median      3Q     Max 
# -2.2591 -0.6236 -0.0772  0.5388  3.4795 
# 
# Random effects:
#  Groups   Name        Variance Std.Dev.
#  scenario (Intercept) 219.5    14.81   
#  subject  (Intercept) 615.6    24.81   
#  Residual             645.9    25.41   
# Number of obs: 83, groups:  scenario, 7; subject, 6
# 
# Fixed effects:
#             Estimate Std. Error       df t value Pr(>|t|)    
# (Intercept)  256.846     16.116    5.432  15.938 9.06e-06 ***
# attitudepol  -19.721      5.584   70.054  -3.532 0.000735 ***
# genderM     -108.516     21.013    4.007  -5.164 0.006647 ** 
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Correlation of Fixed Effects:
#             (Intr) atttdp
# attitudepol -0.173       
# genderM     -0.652  0.004

21 / 47

Understanding the output

politeness.model0 (top) politeness.model (bottom)

Scenario (item) has much less variability than subject.

Residual: The “random” deviations from the predicted values that are not due to subjects and items, $ϵ$ .

The variation that’s associated with the random effect “subject” dropped considerably $\to$ gender was confounded with the variation that is due to subject.

Random effects

Random effects:
  Groups   Name        Variance Std.Dev.
  scenario (Intercept)  219     14.80   
  subject  (Intercept) 4015     63.36   
  Residual              646     25.42   
Number of obs: 83, groups:  scenario, 7; subject, 6

Random effects:
  Groups   Name        Variance Std.Dev.
  scenario (Intercept) 219.5    14.81   
  subject  (Intercept) 615.6    24.81   
  Residual             645.9    25.41   
Number of obs: 83, groups:  scenario, 7; subject, 6

22 / 47

shifted a considerable amount of the variance that was previously in the random effects component(differences between male and female individuals) to the fixed effects component

Understanding the output

politeness.model0 (top) politeness.model (bottom)

attitudepol is the slope for the categorical effect of politeness.

Pitch is lower in polite speech than in informal speech, by about 20 Hz.

lmer() took whatever comes first in the alphabet to be the reference level.

The second Intercept represents the female for the informal condition.

Fixed effects

Fixed effects:
              Estimate Std. Error t value
  (Intercept)  202.588     26.754   7.572
  attitudepol  -19.695      5.585  -3.527

Fixed effects:
              Estimate Std. Error t value
  (Intercept)  256.846     16.116  15.938
  attitudepol  -19.721      5.584  -3.532
  genderM     -108.516     21.013  -5.164

23 / 47

Understanding the output

Coding schemes

A categorical variable of $n$ levels is entered into a regression analysis as a sequence of $n - 1$ variables. Generally or by default in R, we use dummy coding for them.

contrasts(data$attitude)

#     pol
# inf   0
# pol   1

# change the reference level
contrasts(data$attitude) = contr.treatment(2, base = 2)
contrasts(data$attitude)

#     1
# inf 1
# pol 0

There are also other coding schemes such as effects coding including contrast coding, sum coding and Helmert coding. Different coding system may help answer different research questions. It also greatly changes the way you interpret your output.

24 / 47

Understanding the output

Statistical significance

Unfortunately, p-values for mixed models aren’t as straightforward as they are for the linear model. There are multiple approaches, and there’s a discussion surrounding these, with sometimes wildly differing opinions about which approach is the best.

There is a package lmerTest that provides $p$ values in type I, II or III anova and summery tables for lmer model fits via Satterthwaite's degrees of freedom method or Kenward-Roger method.

library(lmerTest)
politeness.model = lmer(frequency ~ attitude + gender + (1|subject) + (1|scenario), data=data)
anova(politeness.model)

# Type III Analysis of Variance Table with Satterthwaite's method
#           Sum Sq Mean Sq NumDF  DenDF F value    Pr(>F)    
# attitude  8056.2  8056.2     1 70.054  12.473 0.0007351 ***
# gender   17225.2 17225.2     1  4.007  26.669 0.0066467 ** 
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

25 / 47

The F-value is actually the quotient of the ratio: effect variance/error variance; between-group variance/within-group variance. All of this means that the larger an F-value, the better for you to find a “significant” effect, a consistent pattern that is unlikely due to chance. Now, basically, what we’re doing with an ANOVA is the following: we look at how unexpected an F-value that we obtained in our study is. A very large F-value means that the between-group variance (the effect variance) exceeds the within-group variance (the error variance) by a substantial amount. The p-value then just gives a number to how likely a particular F-value is going to occur, with lower p-values indicating that the probability of obtaining that particular F-value is pretty low.

Understanding the output

Statistical significance

Likelihood Ratio Test as a means to attain $p$ values. Likelihood is the probability of seeing the data you collected given your model.

politeness.null = lmer(frequency ~ gender + (1|subject) + (1|scenario), data=data, REML=FALSE)
politeness.full = lmer(frequency ~ attitude + gender + (1|subject) + (1|scenario), data=data, REML=FALSE)
anova(politeness.null, politeness.full)

# Data: data
# Models:
# politeness.null: frequency ~ gender + (1 | subject) + (1 | scenario)
# politeness.full: frequency ~ attitude + gender + (1 | subject) + (1 | scenario)
#                 npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
# politeness.null    5 816.72 828.81 -403.36   806.72                         
# politeness.full    6 807.10 821.61 -397.55   795.10 11.618  1  0.0006532 ***
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

“… politeness affected pitch ( $χ^{2} (1) = 11.62, p = 0.00065$ ), lowering it by about $19.7 H z \pm 5.6$ (standard errors)...”

26 / 47

Model selection

coef(politeness.model)

# $scenario
#   (Intercept) attitude1   genderM
# 1    223.6187  19.72111 -108.5163
# 2    243.7081  19.72111 -108.5163
# 3    248.5330  19.72111 -108.5163
# 4    257.7546  19.72111 -108.5163
# 5    235.1891  19.72111 -108.5163
# 6    224.9513  19.72111 -108.5163
# 7    226.1215  19.72111 -108.5163
# 
# $subject
#    (Intercept) attitude1   genderM
# F1    223.2175  19.72111 -108.5163
# F2    247.5443  19.72111 -108.5163
# F3    240.6137  19.72111 -108.5163
# M3    265.5072  19.72111 -108.5163
# M4    242.5036  19.72111 -108.5163
# M7    203.3646  19.72111 -108.5163
# 
# attr(,"class")
# [1] "coef.mer"

Random intercept model

We accounted for baseline-differences in pitch, but the effect of politeness is the same for all subjects and items.

What if the effect of politeness might be different for different subjects?

27 / 47

Model selection

Random slope model

politeness.model1 = lmer(frequency~attitude + gender + (1+attitude|subject) + (1+attitude|scenario), data = data)
coef(politeness.model1)

Random intercept model

$subject
   (Intercept) attitude2   genderM
F1    242.9386 -19.72111 -108.5163
F2    267.2654 -19.72111 -108.5163
F3    260.3348 -19.72111 -108.5163
M3    285.2283 -19.72111 -108.5163
M4    262.2248 -19.72111 -108.5163
M7    223.0858 -19.72111 -108.5163

Random slope model (correlated)

$subject
   (Intercept) attitude2   genderM
F1    243.2804 -20.49940 -111.1058
F2    267.1173 -19.30447 -111.1058
F3    260.2849 -19.64697 -111.1058
M3    287.1024 -18.30263 -111.1058
M4    264.6698 -19.42716 -111.1058
M7    226.3911 -21.34605 -111.1058

Despite individual variation, there is also consistency in how politeness affects the voice: for all of our speakers, the voice tends to go down when speaking politely, but for some people it goes down slightly more so than for others.

28 / 47

The effect of politeness (attitudepol) is different for each subject and item. It’s always negative and many of the values are quite similar to each other.

Model selection

Interaction terms

An interaction, attitude:sex, occurs when one variable changes how another variable affects the response variable. Alternative notation: attitude*sex = attitude + sex + attitude:sex

Correlation between intercepts and slopes

Using || in (1 + attitude || subject) for example, you are forcing the correlation between the random slopes and the intercepts to be zero.

Overfitting

overfitting occurs when your model has too small a sample size and too many predictor variables. You may get a warning / error that your model wouldn’t converge.

29 / 47

Model selection

How to choose your model?

Depend on your research question and data structure

Exploratory VS confirmatory context
Design variables (theoretical interests) VS control variables
Data-driven (e.g. improve the model fit) VS Design-driven
Top-down VS Bottom-up

Some prefer to proceed incrementally, taking time to examine data.
One should always be cautious of creating a model that is too complex.
Some researchers have shown via simulations that mixed models without random slopes have a relatively high Type I error rate (Schielzeth & Forstmeier, 2009; Barr, Levy, Scheepers, & Tilly, 2013)
Barr et al. (2013) recommend that you should “keep it maximal” with respect to your random effects structure, at least for controlled experiments.

30 / 47

We were not interested in gender differences, but they are well worth controlling for. This is why we had random slopes for the effect of attitude (by subjects and item) but not gender.

If you have predictors that represent control variables, over which you do not intend to perform statistical tests, it is unlikely that random slopes are needed.

Model selection

Limitations

"Singular fit" warning or "not converging" error

We need to simplify our model and remove the random slopes or insignificant terms ( step() does it automatically for you).

But what if we believe there might be some merit to having subject-specific slopes?

Bayes to the rescue

Bayesian mixed effects method are powerful alternatives to more commonly used Frequentist approaches.

31 / 47

There are two major approaches to fit the model parameters. The principle of maximum likelihood: pick parameter values that maximize the probability of your data Y.

Bayesian inference: put a probability distribution on the model parameters and update it on the basis of what parameters best explain the data.

Shrinkage in linear mixed models32 / 47

Shrinkage in linear mixed models

Data

Complete pooling

No pooling

Partial pooling

32 / 47

Data

Research question

The effects of sleep deprivation on psychomotor performance / reaction time (Belenky et al., 2003)

Multilevel data with continuous predictor

	Reaction	Days	Subject
1	249.56	0	308
2	258.7047	1	308
3	250.8006	2	308
4	321.4398	3	308

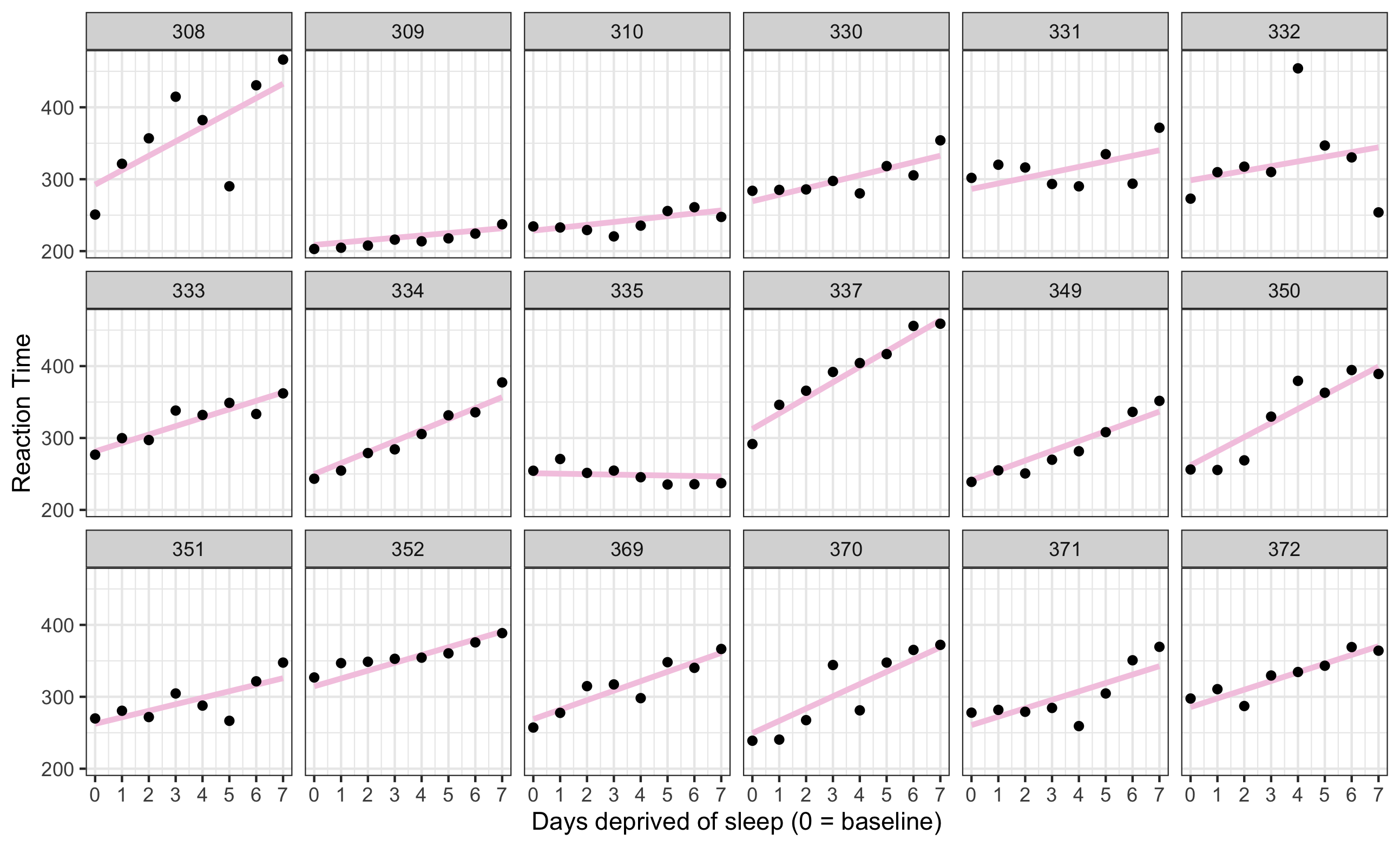
Plot the data

sleep2 <- sleepstudy %>%
  filter(Days >= 2) %>%
  mutate(days_deprived = Days - 2)
ggplot(sleep2, aes(x = days_deprived, 
                   y = Reaction)) +
  geom_point() +
  scale_x_continuous(breaks = 0:7) +
  facet_wrap(~Subject) +
  labs(y = "Reaction Time", 
       x = "Days deprived of sleep (0 = baseline)")

Documentation for the dataset ?sleepstudy

33 / 47

Complete pooling

One-size-fit-all: this approach estimates a single intercept and slope for the entire dataset, ignoring the fact that different subjects might vary in their intercepts or slopes.

It assumes that all observations are independent.

$R T = β_{0} + β_{1} D a y + e$

cp_model <- lm(Reaction ~ days_deprived, sleep2)
summary(cp_model)

ggplot(sleep2, aes(x = days_deprived, y = Reaction)) +
  geom_abline(intercept = coef(cp_model)[1],
              slope = coef(cp_model)[2],
              color = '#f4cae2', size = 1.5) +
  geom_point() +
  scale_x_continuous(breaks = 0:7) +
  facet_wrap(~Subject, nrow = 3) +
  labs(y = "Reaction Time", 
       x = "Days deprived of sleep (0 = baseline)")

34 / 47

Complete pooling

One-size-fit-all: this approach estimates a single intercept and slope for the entire dataset, ignoring the fact that different subjects might vary in their intercepts or slopes.

It assumes that all observations are independent.

$R T = β_{0} + β_{1} D a y + e$

35 / 47

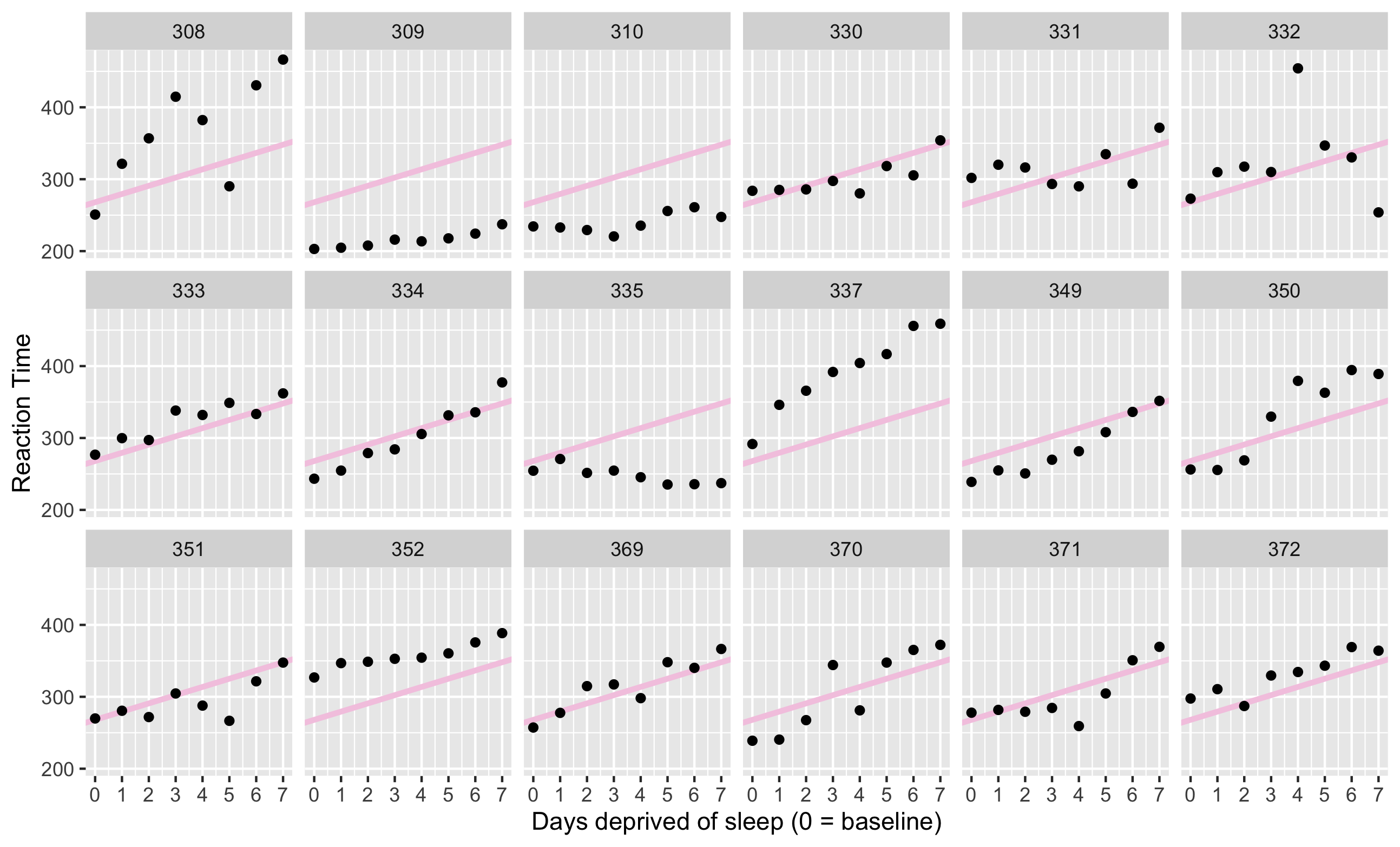
No pooling

This approach fits separate lines for each participant. The estimate for each participant will be completely uninformed by the estimates for the other participants.

There is no overall population intercept and slope that is being estimated.

(1) Run separate regressions for each participant

(2) Run multiple regression

sleep2 %>% pull(Subject) %>% is.factor()
np_model <- lm(Reaction ~ days_deprived + Subject + days_deprived:Subject,
               data = sleep2)
  summary(np_model)
all_intercepts <- c(coef(np_model)["(Intercept)"],
                    coef(np_model)[3:19] + coef(np_model)["(Intercept)"])
all_slopes  <- c(coef(np_model)["days_deprived"],
                 coef(np_model)[20:36] + coef(np_model)["days_deprived"])
ids <- sleep2 %>% pull(Subject) %>% levels() %>% factor()
np_coef <- tibble(Subject = ids,
                  intercept = all_intercepts,
                  slope = all_slopes)

36 / 47

No pooling

multiple regression

This approach fits separate lines for each participant. The estimate for each participant will be completely uninformed by the estimates for the other participants.

There is no overall population intercept and slope that is being estimated.

ggplot(sleep2, aes(x = days_deprived, y = Reaction)) +
  geom_abline(data = np_coef,
              mapping = aes(intercept = intercept,
                            slope = slope),
              color = '#f4cae2', size = 1.5) +
  geom_point() + theme_bw() +
  scale_x_continuous(breaks = 0:7) +
  facet_wrap(~Subject, nrow=3) +
  labs(y = "Reaction Time", 
       x = "Days deprived of sleep (0 = baseline)")

37 / 47

No pooling

multiple regression

This approach fits separate lines for each participant. The estimate for each participant will be completely uninformed by the estimates for the other participants.

There is no overall population intercept and slope that is being estimated.

38 / 47

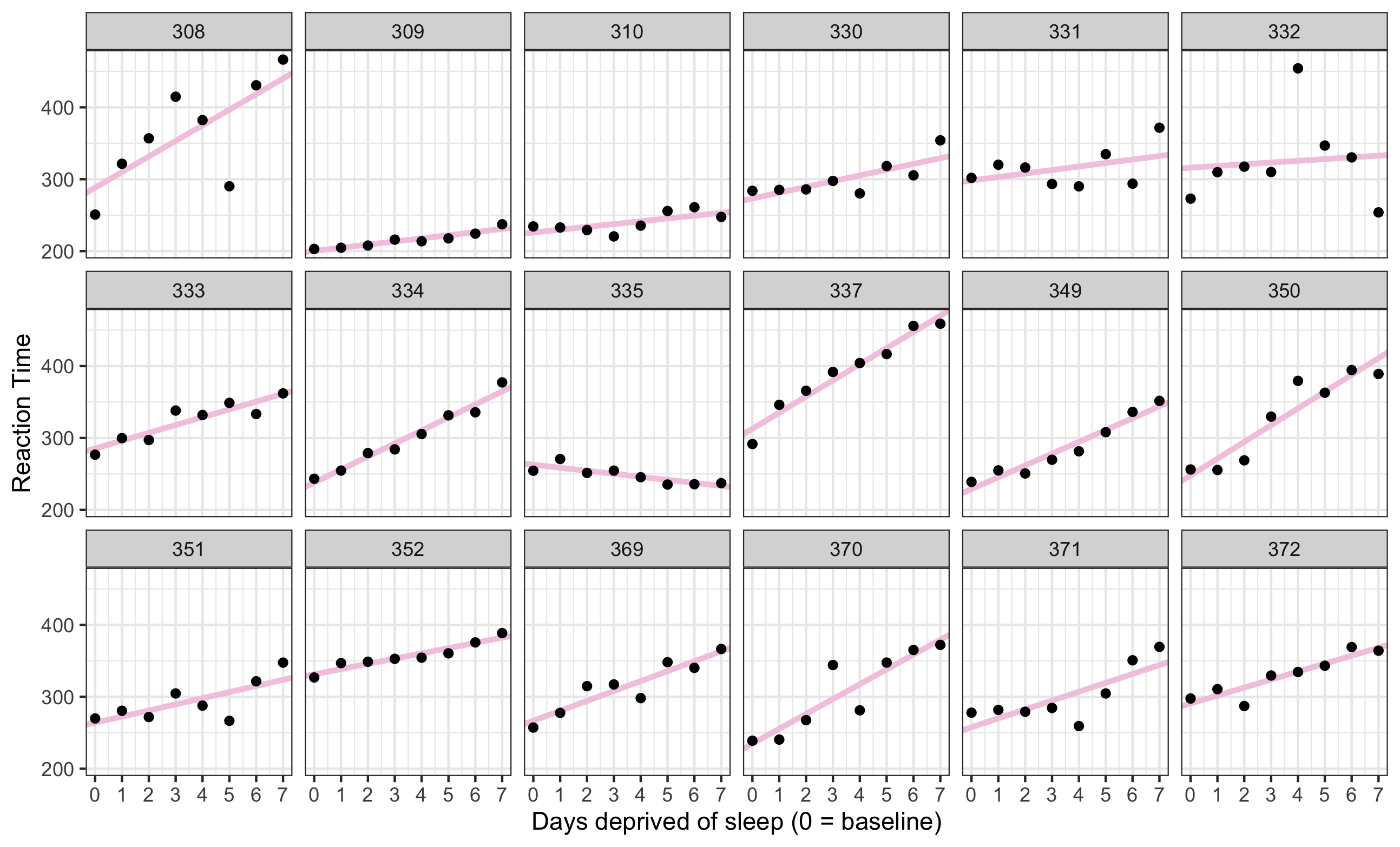
No pooling

multiple regression

This approach fits separate lines for each participant. The estimate for each participant will be completely uninformed by the estimates for the other participants.

There is no overall population intercept and slope that is being estimated.

A one-sample t-test:

np_coef %>% pull(slope) %>% t.test()

# 
#     One Sample t-test
# 
# data:  .
# t = 6.1971, df = 17, p-value = 9.749e-06
# alternative hypothesis: true mean is not equal to 0
# 95 percent confidence interval:
#   7.542244 15.328613
# sample estimates:
# mean of x 
#  11.43543

The mean slope of 11.435 is significantly different from zero, $t (17) = 6.197, p < .001$ .

39 / 47

Partial pooling

It would be desirable to improve our estimates for individual participants by taking advantage of what we know about the other participants.

It would improve generalization to the population.

We are interested in the 18 subjects as examples drawn from a larger population of potential subjects.

LME model estimates values for the population, and pulls the estimates for individual subjects toward those values, a statistical phenomenon known as shrinkage.

Level 1 (for subject $i$ ):

$R T_{i} = β_{0 i} + β_{1 i} D a y_{i} + e_{i}$

Level 2 (for subject $i$ ):

$β_{0 i} = γ_{0} + S u b j e c t_{0 i}$ $β_{1 i} = γ_{1} + S u b j e c t_{1 i}$

40 / 47

Partial pooling happens when you treat a factor as a random instead of fixed in your analysis.

Partial pooling

It would be desirable to improve our estimates for individual participants by taking advantage of what we know about the other participants.

It would improve generalization to the population.

We are interested in the 18 subjects as examples drawn from a larger population of potential subjects.

pp_mod <- lmer(Reaction ~ days_deprived + (days_deprived | Subject), sleep2)
summary(pp_mod)
newdata <- crossing(
  Subject = sleep2 %>% pull(Subject) %>% levels() %>% factor(),
  days_deprived = 0:7)
newdata2 <- newdata %>%
  mutate(Reaction = predict(pp_mod, newdata))

ggplot(sleep2, aes(x = days_deprived, y = Reaction)) +
  geom_line(data = newdata2,
            color = '#f4cae2', size = 1.5) +
  geom_point() + theme_bw() +
  scale_x_continuous(breaks = 0:7) +
  facet_wrap(~Subject, nrow = 3) +
  labs(y = "Reaction Time", 
       x = "Days deprived of sleep (0 = baseline)")

41 / 47

Partial pooling

It would be desirable to improve our estimates for individual participants by taking advantage of what we know about the other participants.

It would improve generalization to the population.

We are interested in the 18 subjects as examples drawn from a larger population of potential subjects.

42 / 47

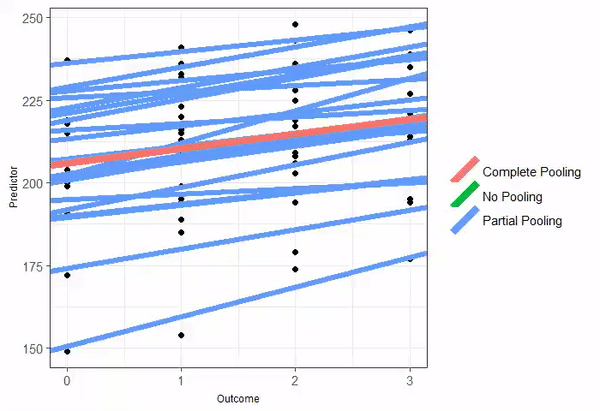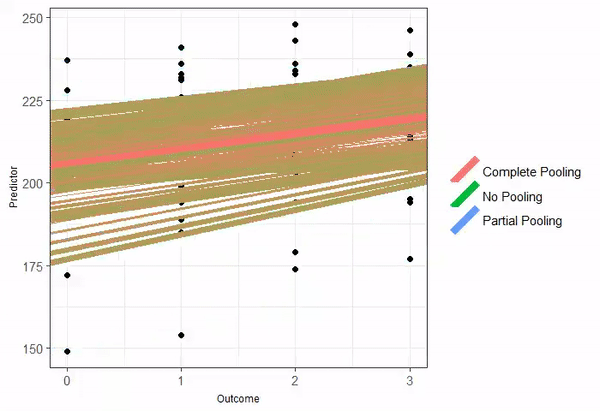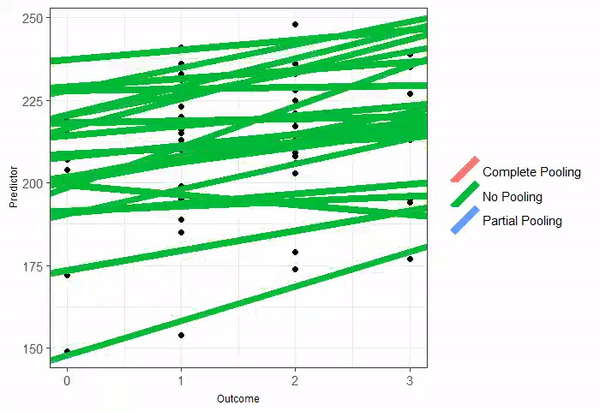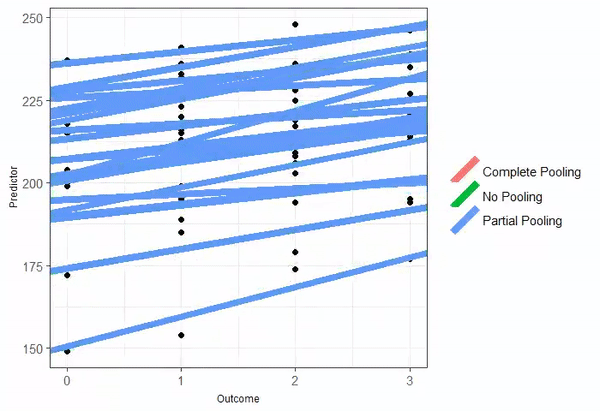
Partial pooling

When partial-pooling goes wrong...

Vanishing confidence intervals (the model is too complex for the data to support).
Unintended Shrinkage.¹
- In 2016, George et al. showed that partial pooling can lead to artificially low predicted mortality rates for smaller hospitals.
The number of random effect levels has a strong impact on the uncertainty of the estimate variance.²

The estimates are pulled or "shrunk" closer to the overall population average. The animated GIF is from Isabella R. Ghement. Twitter: @IsabellaGhement

¹ https://towardsdatascience.com/when-mixed-effects-hierarchical-models-fail-pooling-and-uncertainty-77e667823ae8 ² https://www.muscardinus.be/2018/09/number-random-effect-levels/

43 / 47

Report writing

Goal: Reproducible

Describe and justify your model (summarize the model fit).
- Specify all fixed and random effects, interactions, intercepts, and slopes
- Specify sample size: number of observations, and number of levels for each grouping factor
Mention that you checked assumptions, and that the assumptions are satisfied.
Fixed effects: Report significance (test statistic, degrees of freedom, $p$ -value) and actual estimates for coefficients (effect size: magnitude and direction, standard errors, and confidence intervals). Report Post-hoc tests (emmeans()).
Random effects: Report the variances, standard deviations, and any correlations for each component
Cite the relevant packages.

(recommended) Basic descriptive statistics (e.g. mean and standard deviation of each group)
(recommended) Plot showing distribution of the data

44 / 47

Post-hoc tests test for differences between (combinations of) levels of a factor x, after fitting the model.

Why LME model?

Multilevel / Hierarchical / Nested data

Within-subject factor? Repeated measures?
Psedoreplications (multiple measurements within the same condition)?
Multiple stimulus items?

Science (causal) model before statistical model

Data types: numerical continuous data or categorical data?
Operational hypothesis?

45 / 47

In the sleepstudy data, you had the within-subject factor of Day (which is more a numeric variable, actually, than a factor; but it has multiple values varying within each participant).

generalized linear model (GLM) η determines the predicted mean μ of Y (link function) The predicted mean is just the linear predictor (linear regression)

take a step back (McElreath, 2022)

References

Winter, B. (2013). Linear models and linear mixed effects models in R with linguistic applications. arXiv:1308.5499. [http://arxiv.org/pdf/1308.5499.pdf]

Shravan Vasishth, Daniel Schad, Audrey Bürki, Reinhold Kliegl. (on going) Linear Mixed Models in Linguistics and Psychology: A Comprehensive Introduction. [https://vasishth.github.io/Freq_CogSci/]

Barr, Dale J. (2021). Learning statistical models through simulation in R: An interactive textbook. Version 1.0.0. Retrieved from https://psyteachr.github.io/stat-models-v1.

McElreath, R. (2020). Statistical Rethinking: A Bayesian course with examples in R and STAN. CRC Press.

Thanks!

Slides created via the R package xaringan.

The chakra comes from remark.js, knitr, and R Markdown.

47 / 47

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help

Linear Mixed Effects Models in R

An introduction for linguistic students

Chenzi Xu

University of Oxford

2021/12/12 (updated: 2022-02-18) chenzi.xu@rbind.io

Find me at...

Did you do the pre-workshop setup?

We assume:

You want to know more about linear mixed models

Outline

Inferential Stats Recap

Inferential Stats Recap

Central limit theorem (magic)

Definition and Significance

Hypothesis testing: the (humble) t-test

NHST procedure

Hypothesis testing: the (humble) t-test

Linear Regression

Linear Regression

Formal forms

A simple case study

Research question

Data

Formula

Understanding output

Reporting:

Understanding output

Assumptions check

(1) Linearity

Assumptions check

(2) Absence of collinearity

(3) Homoskedasticity

Assumptions check

(4) Absence of influential data points

Assumptions check

(5) Normality of residuals

(6) Independence

Linear Mixed Effects Model

Linear Mixed Effects Model

Data

Research Question

Model

Model in R

Understanding the output

politeness.model0 (top) politeness.model (bottom)

Random effects

Understanding the output

politeness.model0 (top) politeness.model (bottom)

Fixed effects

Understanding the output

Coding schemes

Understanding the output

Statistical significance

Understanding the output

Statistical significance

Model selection

Random intercept model

Model selection

Random slope model

Model selection

Interaction terms

Correlation between intercepts and slopes

Overfitting

Model selection

How to choose your model?

Model selection

Limitations

"Singular fit" warning or "not converging" error

Bayes to the rescue

Shrinkage in linear mixed models

Shrinkage in linear mixed models

Data

Research question

Multilevel data with continuous predictor

Plot the data

Complete pooling

Complete pooling

No pooling

No pooling

No pooling

2021/12/12 (updated: 2022-02-18)

chenzi.xu@rbind.io

Level 1 (for subject $i$ ):

Level 2 (for subject $i$ ):